Calculus: A Comprehensive Approach – Graphical, Numerical, and Algebraic
Today, February 12, 2026, access to a vast collection of 500,000 books is urgently needed; explore graphical, numerical, and algebraic calculus resources in PDF format.
Calculus, a powerful mathematical tool, fundamentally explores change. It’s built upon three interconnected approaches: graphical understanding, numerical approximation, and algebraic manipulation. This course emphasizes mastering all three, often utilizing readily available PDF resources for comprehensive study.
We’ll investigate functions and their rates of change, utilizing visual representations to solidify concepts. Numerical methods provide practical solutions when analytical approaches are challenging. Algebraic techniques form the bedrock for precise calculations and proofs. The current urgency to restore access to 500,000 books highlights the importance of open access to these vital learning materials. Expect a blend of theory and application, preparing you for advanced mathematical pursuits and real-world problem-solving.
The Historical Development of Calculus
The seeds of calculus were sown long before Newton and Leibniz, with contributions from ancient Greek mathematicians exploring infinitesimals. However, the 17th century witnessed a pivotal shift, driven by the need to solve problems in physics and astronomy. Early methods were largely geometrical, relying on visual representations – a graphical approach.
As precision increased, numerical techniques emerged for approximating solutions. Simultaneously, algebraic formulations provided a rigorous framework. Today, accessing historical texts, often available as PDFs, is crucial. The recent plea to restore access to 500,000 books underscores the importance of preserving this intellectual heritage. Understanding this evolution provides context for modern applications and methodologies.
Newton and Leibniz: Independent Discoveries
Isaac Newton and Gottfried Wilhelm Leibniz, working independently, revolutionized mathematics with the development of calculus. Newton, focused on physics, conceived of ‘fluxions’ – rates of change – visualized through graphical methods. Leibniz, with a more algebraic bent, formalized the notation we largely use today, emphasizing infinitesimal quantities.
Both approached problems using numerical approximations initially, before establishing rigorous frameworks. Access to their original papers, often found as PDFs, reveals their distinct yet complementary approaches. The current effort to restore access to 500,000 books highlights the importance of preserving these foundational works. Their discoveries laid the groundwork for modern analysis and applications.
Early Applications and Evolution
Following Newton and Leibniz, calculus rapidly expanded, finding applications in physics, astronomy, and engineering. Early mathematicians refined graphical interpretations and developed numerical methods for solving complex problems; The need for accessible resources spurred the creation of textbooks, some now available as PDFs, detailing algebraic techniques.
The Internet Archive’s current struggle to restore access to 500,000 books underscores the importance of preserving this historical evolution. These texts demonstrate how calculus moved from a tool for elite scientists to a cornerstone of modern education. Continued access to these resources is vital for understanding the field’s development.

Foundations: Functions and Limits
February 12, 2026, demands restoring access to 500,000 books; explore functions, limits, and their graphical, numerical, and algebraic representations in available PDFs.
Understanding Functions: Domain, Range, and Graphs
As of February 12, 2026, the urgent need to restore access to 500,000 books highlights the importance of readily available educational resources. Understanding functions is foundational to calculus, requiring a grasp of their domain – the input values – and range, the resulting output values.
Graphical representations visually depict these relationships, while numerical methods, like tables, offer discrete data points. Algebraic definitions provide the formal rules governing the function. Exploring these facets, ideally through accessible PDF materials, is crucial.
Visualizing functions through graphs aids in understanding concepts like continuity and limits. Access to comprehensive resources, including textbooks and online tools, is paramount for mastering these core principles. The Internet Archive’s potential restoration is vital for students and educators alike.
Limits: The Foundation of Calculus
Considering the pressing need, as of February 12, 2026, to reinstate access to 500,000 books, readily available learning materials are essential. Limits form the bedrock of calculus, defining how a function behaves as its input approaches a specific value.
Graphical analysis allows visualization of limit behavior, while numerical approaches, using tables, approximate limit values. Algebraic techniques, like factoring and simplification, determine limits analytically; Accessible PDF resources are invaluable for practice.
Understanding limits is crucial for grasping continuity, derivatives, and integrals. The Internet Archive’s potential restoration of resources would significantly benefit students studying these fundamental concepts, providing wider access to vital calculus knowledge.
One-Sided Limits
With the urgent plea, dated February 12, 2026, to restore access to 500,000 books, comprehensive learning resources are paramount. One-sided limits examine a function’s behavior as the input approaches a value from either the left or the right.
Graphical representations clearly illustrate approaching values from specific directions. Numerical tables can demonstrate differing function values from each side. Algebraic manipulation helps determine if one-sided limits exist and are equal.
These limits are vital when dealing with piecewise functions or functions with discontinuities. Accessible PDF materials and online tools are crucial for mastering this concept. The Internet Archive’s potential restoration would greatly aid calculus students’ understanding.
Limits at Infinity
Considering the critical need, as of February 12, 2026, to reinstate access to 500,000 books, robust learning materials are essential. Limits at infinity describe a function’s behavior as the input grows without bound, either positively or negatively.
Graphical analysis reveals horizontal asymptotes, indicating the function’s long-term trend. Numerical exploration with large input values demonstrates approaching limits. Algebraic techniques, like dividing by the highest power, simplify limit evaluation.
Understanding these limits is crucial for analyzing end behavior and asymptotic behavior. Accessible PDF resources and online calculators are invaluable. The Internet Archive’s restoration would significantly benefit calculus learners.
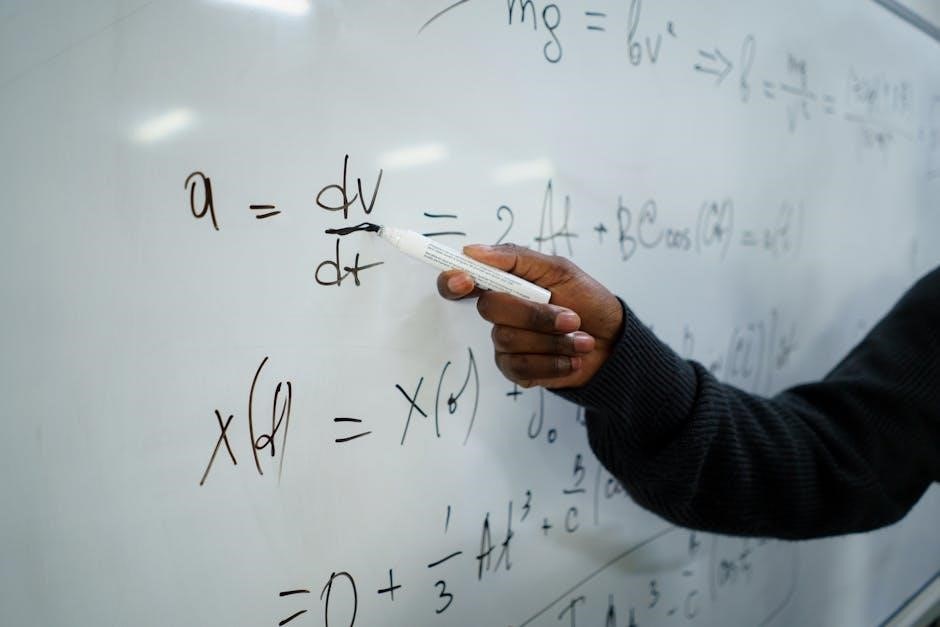
Differential Calculus
February 12, 2026, demands restored access to 500,000 books; explore differential calculus graphically, numerically, and algebraically via available PDF resources.
The Derivative: Rate of Change
As of February 12, 2026, the urgent need to restore access to 500,000 books highlights the importance of readily available learning resources. The derivative, fundamentally, represents the instantaneous rate of change of a function. Graphically, this is the slope of the tangent line at a specific point on the function’s curve.
Numerically, we approximate the derivative using difference quotients, calculating the change in y divided by the change in x. Algebraically, the derivative is found using defined rules – power rule, product rule, and quotient rule – allowing for precise calculations. PDF resources containing detailed examples and practice problems are crucial for mastering these concepts. Understanding the derivative is pivotal for optimization, related rates, and curve sketching, all enhanced by graphical and numerical interpretations.
Differentiation Rules: Power, Product, and Quotient Rules
Reflecting today’s date, February 12, 2026, the accessibility of 500,000 books underscores the need for comprehensive calculus materials. Mastering differentiation requires understanding core rules. The power rule simplifies differentiating terms like xn. The product rule handles functions multiplied together: (uv)’ = u’v + uv’.
The quotient rule addresses functions divided by each other: (u/v)’ = (u’v ౼ uv’)/v2. Graphical representations visually demonstrate how these rules affect function slopes. Numerical methods offer approximations, while algebraic manipulation provides exact solutions. PDF guides with worked examples are invaluable. These rules, combined with graphical and numerical insights, form the bedrock of calculus proficiency.
Chain Rule and Implicit Differentiation
As of February 12, 2026, the urgent plea to restore access to 500,000 books highlights the importance of readily available learning resources. The chain rule tackles composite functions: d/dx[f(g(x))] = f'(g(x)) * g'(x). It’s crucial for complex function differentiation.
Implicit differentiation handles equations where y isn’t explicitly solved for x, using dy/dx. Graphical tools visualize these concepts, showing tangent lines. Numerical approximations aid in complex scenarios. Algebraic skills are vital for manipulation. PDF resources offering step-by-step solutions are essential. Combining these approaches – graphical, numerical, and algebraic – provides a robust understanding of these powerful techniques.

Applications of Derivatives
Today, February 12, 2026, the need to reinstate access to 500,000 books underscores the value of accessible educational materials. Derivatives find practical use in determining rates of change, crucial for modeling real-world phenomena. Graphical analysis reveals function behavior – increasing/decreasing intervals, maxima/minima.
Numerical methods approximate solutions when analytical approaches are difficult. Algebraic skills are fundamental for setting up and solving derivative-based problems. PDF guides provide worked examples. Combining graphical interpretation, numerical approximation, and algebraic manipulation offers a comprehensive understanding of derivative applications in physics, engineering, and economics.
Optimization Problems
Today, February 12, 2026, the urgent call to restore 500,000 books highlights the importance of readily available learning resources. Optimization problems utilize derivatives to find maximum or minimum values of functions, representing real-world constraints. Graphical methods visualize feasible regions and potential solutions.
Numerical techniques refine approximate solutions, while algebraic skills are essential for formulating objective functions and constraints. PDF resources offer step-by-step guidance. A combined approach – graphical understanding, numerical refinement, and algebraic precision – empowers effective problem-solving in fields like engineering, economics, and resource allocation.
Related Rates
Today, February 12, 2026, the plea to reinstate access to 500,000 books underscores the need for accessible educational materials. Related rates problems explore how the rates of change of different variables are connected. These problems demand implicit differentiation and a strong understanding of chain rule applications.
Graphical representations can illustrate the changing relationships, while numerical methods approximate rates when analytical solutions are complex. Algebraic manipulation is crucial for establishing equations linking variables. PDF guides provide worked examples. Mastering related rates requires a synthesis of graphical intuition, numerical approximation, and robust algebraic skills.
Curve Sketching and Analysis
Today, February 12, 2026, the urgent call for restoring 500,000 books highlights the importance of readily available learning resources. Curve sketching involves analyzing a function’s behavior to accurately depict its graph. This process utilizes derivatives to find critical points, intervals of increase/decrease, and concavity.
Graphical tools visualize these features, while numerical methods approximate function values. Algebraic techniques determine asymptotes and intercepts. Comprehensive PDF guides offer step-by-step examples. Effective curve sketching blends graphical interpretation, numerical estimation, and precise algebraic calculations, providing a complete function analysis.
Integral Calculus
Today, February 12, 2026, urgently seeking access to 500,000 books, integral calculus utilizes graphical, numerical, and algebraic methods, often found in PDF resources.
The Integral: Accumulation and Area
As of February 12, 2026, the integral represents a fundamental concept in calculus, extending beyond simple area calculations to embody the idea of accumulation. Graphically, it’s visualized as the area under a curve, offering a powerful tool for understanding change. Numerical methods, alongside algebraic techniques, provide ways to approximate integrals when analytical solutions are elusive.
Access to resources, including comprehensive PDF textbooks, is crucial for mastering these concepts. The integral’s application spans diverse fields, from physics and engineering to economics and statistics. Understanding its connection to the derivative, as defined by the Fundamental Theorem of Calculus, is paramount. Exploring graphical representations alongside algebraic manipulations solidifies comprehension.
Fundamental Theorem of Calculus
On February 12, 2026, the Fundamental Theorem of Calculus establishes a crucial link between differentiation and integration – seemingly opposite operations. It states that differentiation and integration are inverse processes, allowing us to calculate definite integrals using antiderivatives. Graphical interpretations demonstrate how the area under a curve relates to the function’s rate of change.
Numerical methods offer approximations when finding antiderivatives algebraically proves difficult. Access to PDF resources detailing proofs and applications is vital. This theorem is foundational for solving numerous problems across science and engineering. Mastering both parts of the theorem – and understanding its implications – is essential for a comprehensive grasp of calculus.
Integration Techniques: Substitution and Integration by Parts
As of February 12, 2026, mastering integration requires a toolkit of techniques. Substitution, often called u-substitution, simplifies integrals by reversing the chain rule. Integration by parts, derived from the product rule, tackles integrals of products of functions. Graphical representations can illustrate how these techniques transform complex integrals into manageable forms.
Numerical approximations become invaluable when analytical solutions are elusive. PDF resources provide detailed examples and practice problems. Algebraic manipulation is key to successful application. These techniques, alongside others, are crucial for solving a wide range of calculus problems, particularly in physics and engineering contexts.
Applications of Integrals
On February 12, 2026, integrals extend far beyond theoretical exercises. They are fundamental for calculating areas between curves, a core geometric application. Furthermore, integrals determine volumes of solids of revolution, vital in engineering and 3D modeling. Graphical interpretations visually demonstrate these calculations, enhancing understanding.
Numerical methods provide approximations when analytical solutions are complex. Accessing PDF resources with worked examples is invaluable. Algebraic skills are essential for setting up and solving integral problems. These applications, combined with others, showcase the power of calculus in diverse fields, from physics to economics.
Area Between Curves
As of February 12, 2026, determining the area enclosed by two or more curves relies heavily on definite integrals; This application beautifully blends graphical understanding with algebraic setup and evaluation. Visualizing the region is crucial; sketching the curves aids in defining integration limits.
Numerical methods offer approximations when curves are complex or intersections are difficult to find analytically. PDF resources provide step-by-step solutions for various scenarios. Mastering algebraic manipulation is key to correctly expressing the integrand. This concept demonstrates calculus’s power in solving real-world geometric problems.
Volumes of Solids of Revolution
On February 12, 2026, calculating volumes generated by revolving curves around an axis utilizes integral calculus, specifically the disk, washer, or shell methods. Graphical representation helps visualize the solid formed, aiding in selecting the appropriate method. Algebraic skills are vital for setting up the integral correctly.
Numerical approximations become valuable for complex shapes where analytical solutions are challenging. PDF guides offer detailed examples and practice problems. Understanding the relationship between the function, the axis of revolution, and the resulting volume is paramount. This showcases calculus’s ability to tackle three-dimensional geometric problems.
Numerical Methods in Calculus
Today, February 12, 2026, explore approximations of derivatives and integrals using techniques like Trapezoidal and Simpson’s Rules, often found in PDF resources.
Numerical Differentiation
As of February 12, 2026, numerical differentiation provides methods to approximate the derivative of a function when an explicit formula is unavailable or computationally expensive. These techniques rely on finite difference approximations, utilizing function values at discrete points. Forward, backward, and central difference formulas are commonly employed, offering varying degrees of accuracy.
Accessing resources in PDF format, alongside graphical and algebraic tools, enhances understanding. The accuracy of numerical differentiation is influenced by the step size; smaller steps generally yield better approximations but can introduce round-off errors. Exploring these methods is crucial for practical applications where analytical solutions are not feasible, and online calculators can aid in visualization and computation.
Numerical Integration: Trapezoidal and Simpson’s Rules
On February 12, 2026, numerical integration techniques, like the Trapezoidal and Simpson’s Rules, approximate definite integrals when analytical solutions are challenging. The Trapezoidal Rule estimates the area under a curve using trapezoids, while Simpson’s Rule employs parabolas for increased accuracy.
PDF resources, combined with graphical representations and algebraic manipulation, solidify comprehension. Simpson’s Rule generally provides a more precise approximation, particularly for smooth functions. The number of subintervals impacts accuracy; more subintervals typically lead to better results but increase computational cost. Online tools and calculators facilitate these calculations, offering visual insights into the integration process.

Calculus Resources: PDF and Online Tools
February 12, 2026, unlocks access to vital calculus PDFs, alongside interactive online calculators and graphing tools for graphical, numerical, and algebraic mastery.

Recommended Calculus Textbooks (PDF Availability)

As of today, February 12, 2026, securing access to comprehensive calculus textbooks is paramount. Many publishers offer digital versions, including PDFs, facilitating study. Consider “Calculus: Early Transcendentals” by James Stewart, often available in PDF format, known for its clear explanations and numerous examples covering graphical, numerical, and algebraic approaches.
Another excellent resource is “Calculus” by Howard Anton, Irl Bivens, and Stephen Davis, providing a solid foundation with a focus on problem-solving. Explore options from Thomas’ Calculus, a classic text with extensive coverage. The Internet Archive, striving to restore access to 500,000 books, may hold valuable older editions. Remember to verify the legality of accessing any PDF before downloading, respecting copyright regulations. Prioritize textbooks that integrate graphical representations, numerical methods, and rigorous algebraic techniques for a well-rounded understanding;
Online Calculus Calculators and Graphing Tools
Today, February 12, 2026, numerous online tools complement calculus study, especially when seeking graphical, numerical, and algebraic insights. Desmos offers a powerful, free graphing calculator, ideal for visualizing functions and limits. Wolfram Alpha excels at symbolic computation, handling derivatives, integrals, and equation solving. Symbolab provides step-by-step solutions, aiding comprehension.
GeoGebra combines geometry, algebra, spreadsheets, and calculus, offering interactive learning. These resources often support PDF-based textbook learning by verifying solutions and exploring concepts visually. While the Internet Archive works to restore access to 500,000 books, these tools provide immediate support. Remember to use these tools to understand concepts, not just obtain answers, strengthening your algebraic and numerical skills.





